Trajectory Optimization

Dojo provides dynamics constraints and Jacobians in order to perform trajectory optimization using iterative LQR.

Quadruped

A Unitree A1 takes a number of forward steps. There are costs on a kinematic gait and control usage, as well as an augmented Lagrangian (i.e., soft) constraint on the the robot's final pose. The maximal representation is converted to a minimal one for optimization. Additionally, slack controls are utilized early on to aid the optimizer before being driven to zero by a constraint to achieve a dynamically feasible trajectory.

Atlas

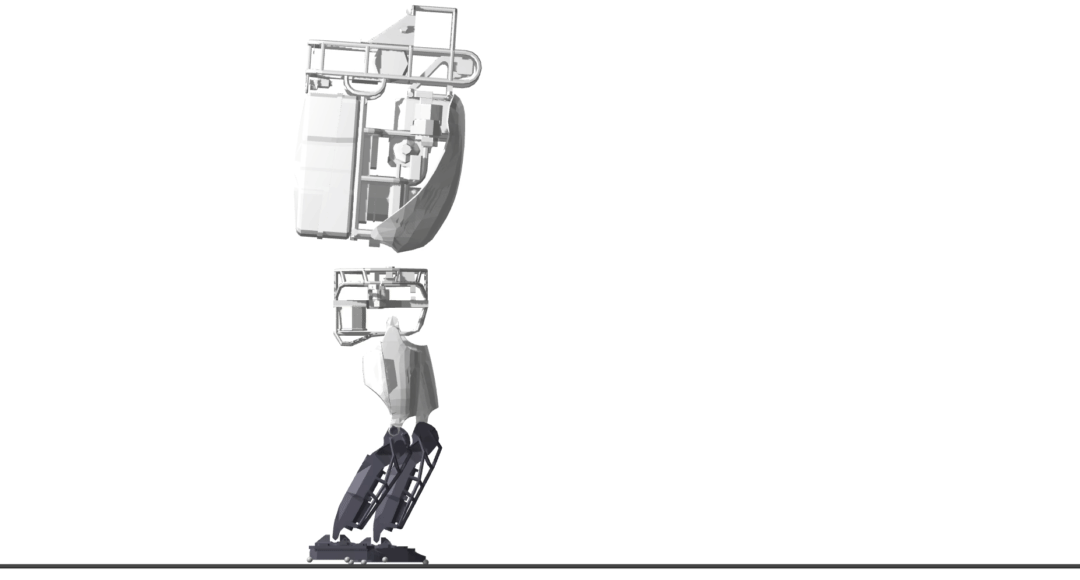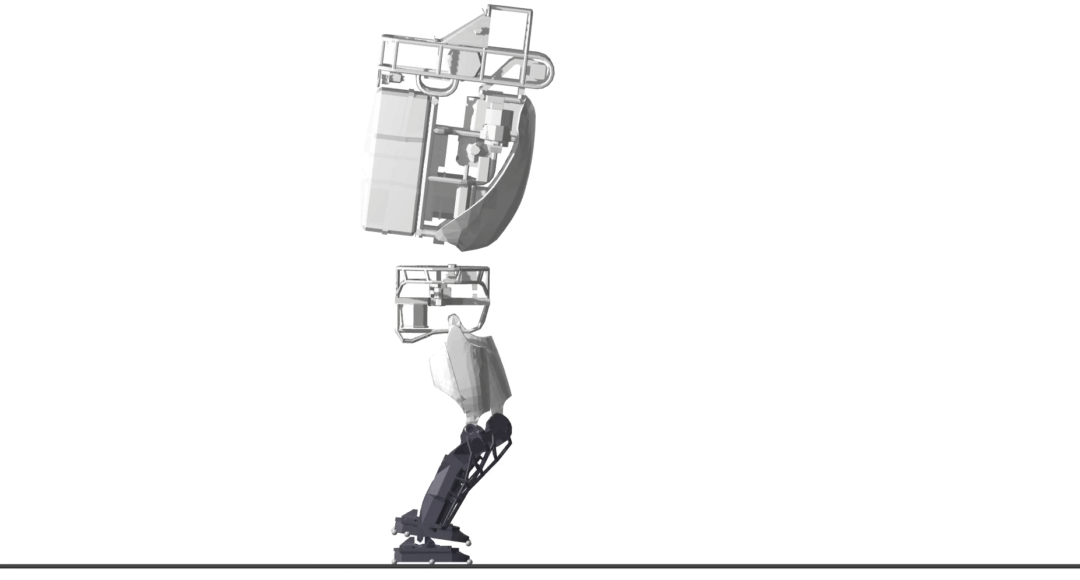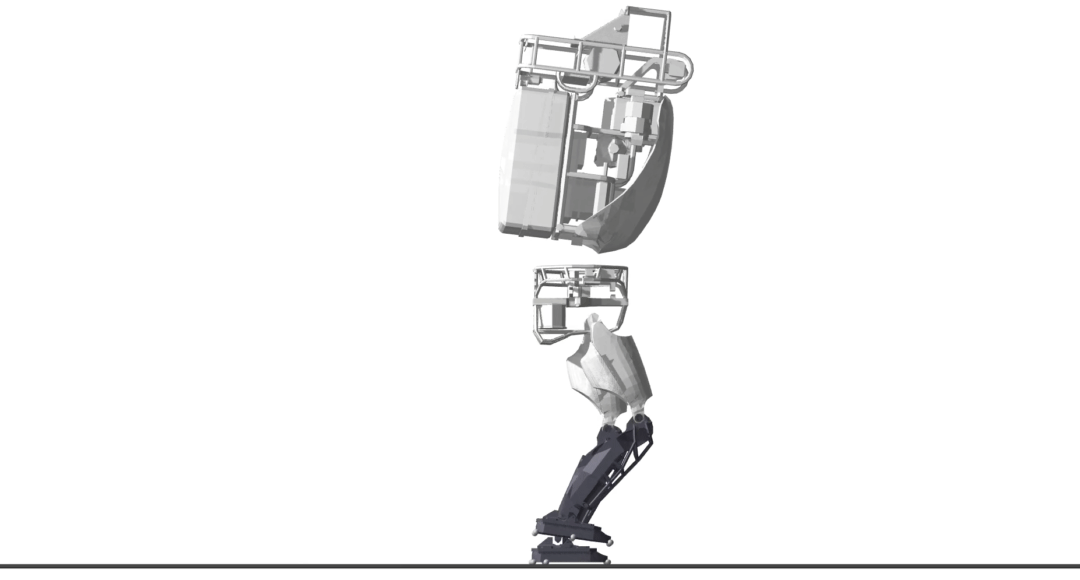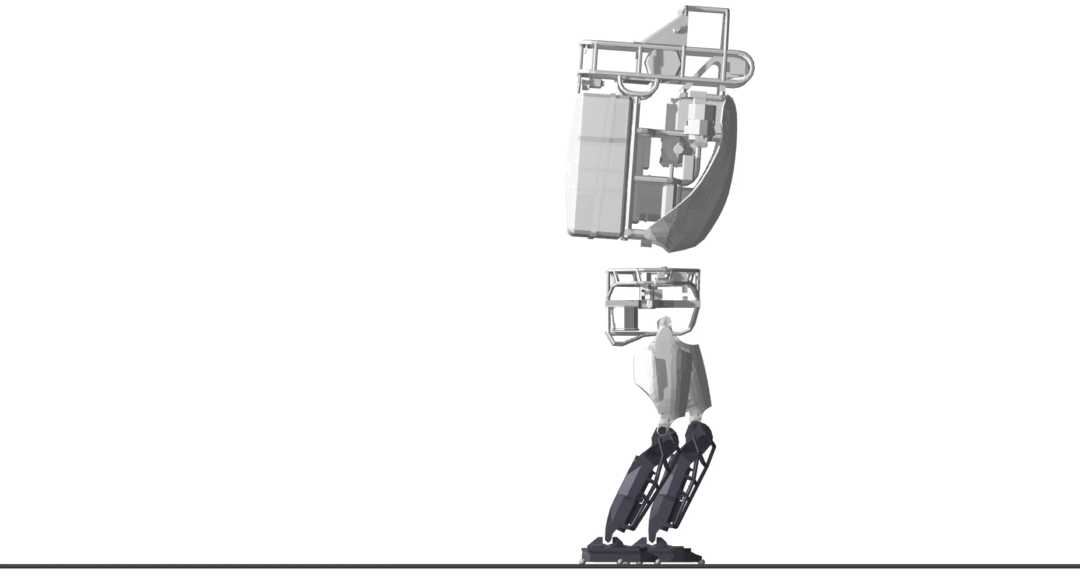
The Atlas v5 humanoid (sans arms) takes a number of forward steps. Similar to the quadruped example, there are costs on control effort and deviations from a kinematic plan, a minimal representation is utilized, and the optimizer is aided by slack controls.

Block

A block is moved to a goal location by applying forces to its center of mass. The optimizer is initialized with zero control and utilizes smooth gradients from Dojo to find a motion that overcomes friction to slide towards the goal.

Raibert Hopper

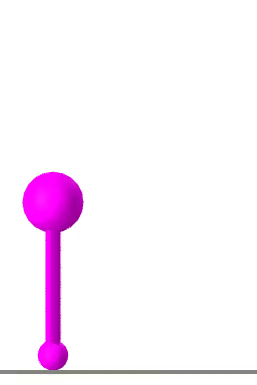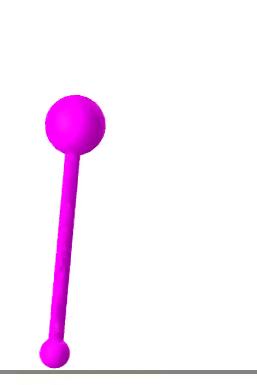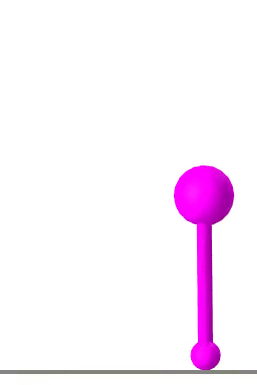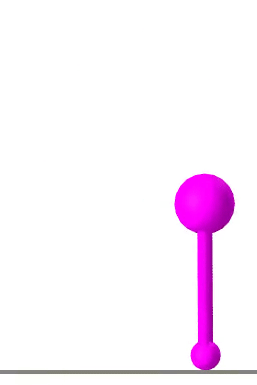
A hopping robot, inspired by the Raibert Hopper, is tasked with moving to a goal location. The optimizer finds a single hop trajectory to reach its goal pose.

Cartpole

This classic system is tasked with performing a swing-up. Examples are provided performing optimization with both maximal and minimal representations.